Monitores: Aulísio,Ivana,Mafalda.
Temas: Definição de função afim; tipos especiais; função constante; gráficos;coeficientes; raiz da função; crescimento e decrescimento; sinal da função afim.
Uma função afim é toda função de variável x que tem como forma
geral a expressão ax+b=0, com a ≠ 0 e, a e b pertencentes aos ℝ.
Funções afim especiais:
Função Linear:
Uma função definida por f: R→R chama-se linear quando existe uma constante a ∈ R tal que f(x) = ax para todo x ∈ R. A lei que define uma função linear é a seguinte:
O gráfico da função linear é uma reta, não perpendicular ao eixo Ox e que cruza a origem do plano cartesiano.
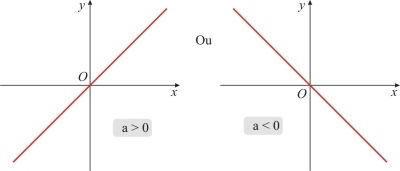
Imagem: Im = R
Função Identidade:
Chama-se função identidade a toda função f: IR → IR definida por:
f(x) = x
Note que a função identidade é um caso particular da função linear f(x) = ax , pois neste caso temos
a = 1 e b = 0.
Chama-se função constante a toda função f: IR → IR definida por:
f(x) = b
onde b ∈ IR. Note que neste caso temos a = 0.
Exercícios:
VÍDEO AULA:
*******************
Valor de uma função afim
Na função afim f(x) = 5x + 1, podemos determinar:
f(1) = 5 • 1 +1 = 5 + 1 = 6. Logo, f(1) = 6.
f(-3)=5(-3) + 1 = -15 + 1 = -14. Logo, f(-3) = -14.
Então o valor da função afim é o valor de f(x) quando substituímos em x um elemento do Domínio da função referida.
BINGO DO VALOR DA FUNÇÃO:
Elaboramos cartelas com 15 pedras cada,e distribuímos entre os alunos. Cada cartela tinha 5 colunas e obviamente 3 linhas.
Procedimento:
Bate o bingo o aluno que conseguir marcar uma linha inteira ou uma coluna inteira. Cada coluna equivale a uma função,e esta função também é sorteada na hora. Após o sorteio da coluna-função,os monitores sorteiam também um elemento do domínio desta função. Desta forma, cada aluno deve rapidamente descobrir o valor da função e marca a imagem na sua cartela.
A equipe : Maria Aparecida,Thaís késsia, Camila Pereira, e Ádina Barbosa , ganhou a brincadeira e levou brindes.
******************
Os alunos visualizaram através do Geogebra como as retas das funções se formam, e depois exercitaram o aprendido no papel milimetrado construindo os vários tipos de gráficos de função polinomial do 1º grau.
Calculadora gráfica on line:
(acesse com o firefox)
******************
ALUNO PIBID,PENSE UM POUCO MAIS NA VIDA PROFISSIONAL,NO SEU FUTURO, ISSO É IMPORTANTE! QUE TAL REFLETIR UM POUCO SOBRE A IMPORTÂNCIA DO ESTUDO NA SUA VIDA? SE MOTIVE,ESTAMOS AQUI PARA ESTIMULAR VOCÊ A ALCANÇAR TODOS OS SEUS OBJETIVOS!
**********************
Para chegar até à lei função a partir de um gráfico de uma função afim é muito simples. Lembremos que f(x)= ax +b. O número b é a imagem do ponto da reta que toca na ordenada,ou seja, o ponto é (0,b) e existe em todo gráfico de função afim. Façamos agora: a= f(x") - f(x').
x" -x'
Dessa forma,vemos que precisamos de poucos pontos para encontrar a tal lei da função. No mínimo dois,no máximo 3,sendo que um seja o ponto (0,b).
DINÂMICA DAS BILAS NO COPO D'ÁGUA:
Esta dinâmica foi realizada após a explanação sobre o conteúdo acima descrito.
Procedimentos:
colocar água em copo até atingir uma altura de
3 cm;
colocar as bolinhas de gude no copo (4 de cada vez) e anotar o resultado;
construir, na folha de papel milimetrado, o gráfico da relação entre x e y;
deduzir uma relação entre x e y, a partir da situação geométrica.
Vamos considerar o número de bolinhas como a variável independente (x) e o nível
de água como a variável dependente (y).
Cada equipe teve de 4 a 5 alunos.
Os pares ordenados obtidos, plotados no plano cartesiano, estão próximos de uma
reta. Para a comprovação de que geometricamente se obtém uma expressão algébrica da forma y=ax+b, basta verificar que a altura do nível de água é igual à soma da altura do nível inicial e a variação da altura à medida que são colocadas as bolinhas. Esse fato é comprovado utilizando a igualdadeVol. do copo = vol. inicial de água + vol. das bolinhas colocadas no copo.
**********************
O coeficiente angular (a) representa a inclinação da reta em relação ao eixo das abscissas (x) e o coeficiente linear (b) representa o valor numérico por onde a reta passa no eixo das ordenadas (y).
O coeficiente angular é a tangente do ângulo formada pela reta da função e o eixo x
f(x)= ax+b
É importante mostrar aos alunos a consequência da variação dos coeficientes angular e linear dentro da lei de uma função. O Geogebra ajuda muito nisso(link para o site um pouco mais acima).
*******************
Raiz da função Afim
A raiz da função é o valor da função quando o elemento do domínio é zero.
exemplo: f(x) = 2x + 1. A raiz da função anterior é calculada da seguinte forma:
2x +1= 0
2x=-1
x = -1/2
Ou seja,a raiz é o elemento do domínio no ponto da reta que toca o eixo x.
A raiz da função, de uma forma geral, uma função afim definida por f(x) =ax +b , terá a seguinte raiz:
CRESCIMENTO E DECRESCIMENTO DA FUNÇÃO AFIM
Crescimento ou decrescimento da função afim
Uma função afim é crescente quando o valor do coeficiente angular for superior a 0 e decrescente quando for inferior.
- a > 0 - função crescente - ângulo agudo
- a < 0 - função decrescente - ângulo obtuso
******************
Estudo do Sinal de uma Função Afim
Estudar a variação do sinal de uma função polinomial do 1° grau nada mais é que identificar para quais valores de x temos f(x) com valor negativo, nulo ou positivo.
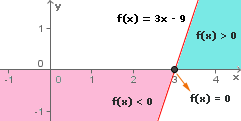
Vamos voltar ao gráfico da função f(x)= 3x -9 e analisá-lo deste outro ponto de vista.
Para valores de x menores que a raiz, isto é, x < 3, vemos quef(x) < 0, pois estes pontos estão abaixo do eixo das abscissas.Para valores de x iguais à raiz temos que a função é nula, isto é,f(x) = 0.Para valores de x maiores que a raiz, ou seja, x > 3, vemos no gráfico que f(x) > 0, já que estes pontos estão acima do eixo das abscissas.
************
DOMINÓ DA FUNÇÃO POLINOMIAL DO 1º GRAU
Nós monitores elaboramos e confeccionamos 3 dominós de E.V.A., com peças em tamanho 5cm X 9cm . As peças contêm : imagem de funções,classificação quanto ao tipo da função e classificação quanto ao crescimento ou decrescimento da função.
Exemplo: se de um lado eu tenho f(x) = -4x perguntando se é crescente ou decrescente, o jogador deverá combinar esse lado da peça com o lado de outra peça que terá a escrito: CRESCENTE.
Contudo,o jogo segue como em um dominó tradicional.
********************
CAMINHO MATEMÁTICO
Consiste na nossa velha cartolina com um caminho desenhado e dividido em casas do tipo ludo. Quatro pinos representam as quatro equipes formadas entre os alunos. O dado dita quantas casas a equipe deve andar no tabuleiro, e cada casa pode ter uma ordem,podendo ser uma pergunta,ou uma surpresa. Cada resposta certa resulta no avanço de 5 casas,cada resposta errada resulta na volta de 3 casas. Ganha a equipe que chegar primeiro à chegada do tabuleiro. Lembrando que as perguntas se encontram nos slides e são exibidas por data show aleatoriamente.
Foi muito bom brincar com os alunos,ver o empenho para ganhar e a alegria dos campeões ,que além de ganharem brindes, mostraram estar por dentro da matéria de função afim.
Campeões: Crystine,Eduarda, Estevão, Tamara, e Débora. Parabéns!
***************
VÍDEO PARÓDIA DA FUNÇÃO AFIM:
Alô vó, já tô passado! :)
***************
VÍDEO PARÓDIA DA FUNÇÃO AFIM:
Alô vó, já tô passado! :)
fontes de pesquisa :
Nenhum comentário:
Postar um comentário